Playing with definitions - Part 1
Definitions from examples - some exercises
There are many things which go into defining an object. This series will focus on one aspect of defining - given examples, some of which are of the object and others which are not, we try to figure out what the definition could be.
In this article, I will pose some questions and address them in future parts of the series.
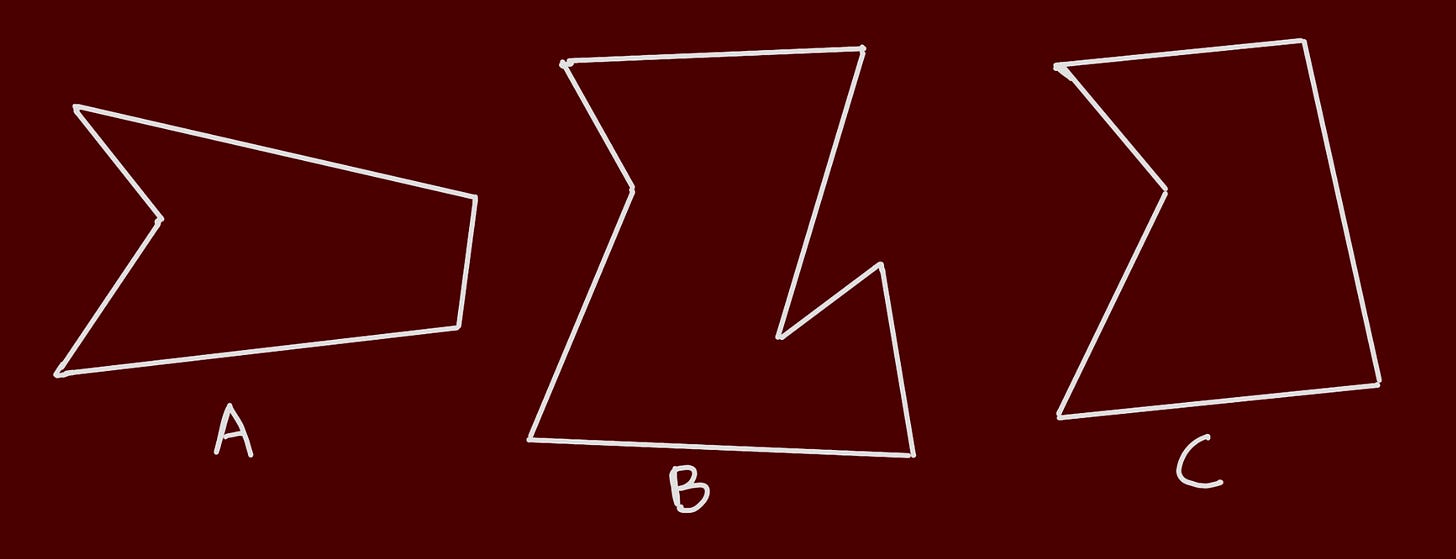
Suppose we were told that there is a type of shape called a ‘podgon’ and suppose the following are examples of podgons.
Now, suppose the following are not podgons:
Given this information, which of the following can be the definition of podgon and which cannot?
A polygon
A polygon with five vertices
A polygon such that at least one diagonal lies outside of it
A polygon with an odd number of vertices
A polygon with an even number of vertices
A polygon such that all the diagonals lie within it
Think about these definitions in light of the examples A-F. I will discuss these in future articles in this series. However, try to play with this on your own before you read those. Make sure to write out your reasoning while doing this.
For those who are unfamiliar with the terminology used above, here are definitions of some of the terms used:
Polygon: A closed shape where all of its sides are straight lines
Vertex: A point at which two adjacent sides (sides next to each other) meet
Diagonal: A line connecting two vertices which are not adjacent (two vertices are adjacent if they share a side)