Learning to classify - part 3
Part 2 can be found here, and Part 1 can be found here. As usual, like this post and share it.
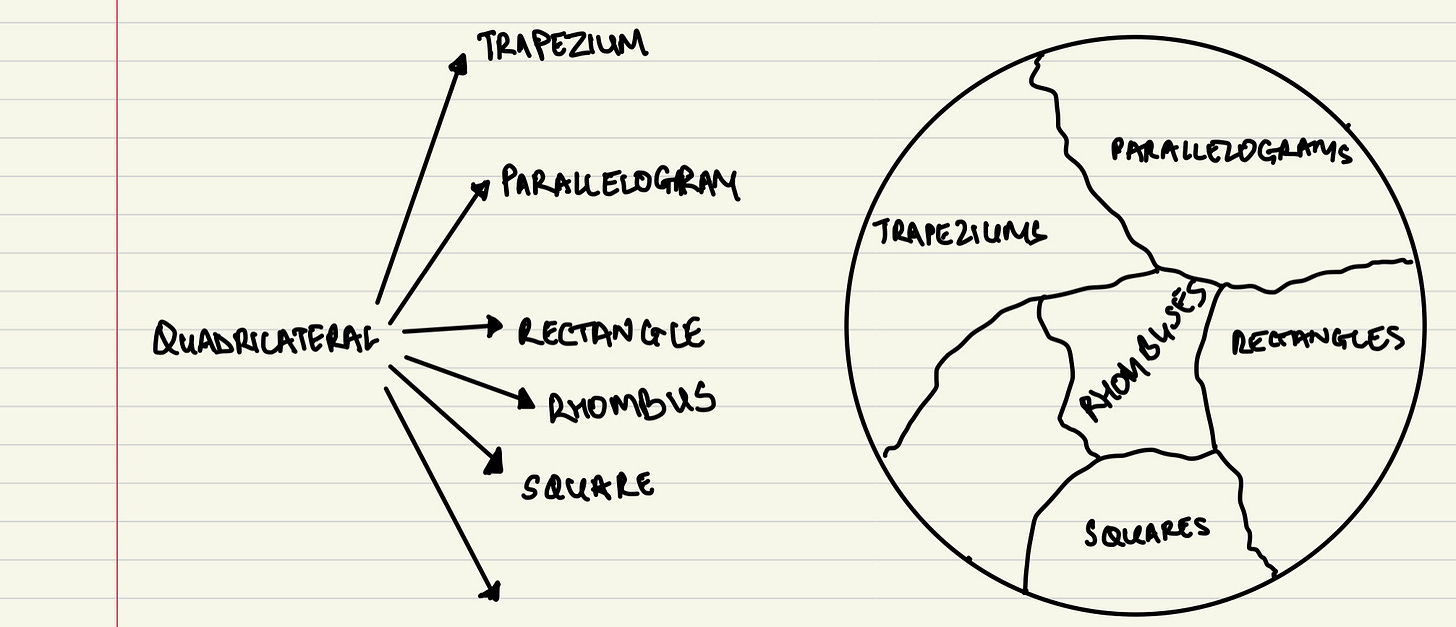
We ended part 2 with Fliba asking Lagard to add rhombuses to the two classificatory systems they were working with. For those who do not remember what a rhombus is, it is a diamond shape with all four sides equal.
Two different representations of these two systems are given below:
Lagard: I tried to add rhombuses into the two systems. I was able to do it for the system on the left where we separate things. Here is the classification for that using both the representations:
But, I’m not sure how to go about doing it in the case of the system on the right.
Fliba: Maybe we should give the systems names. The tree diagram for the right system is very tall so we can call it the skyscraper system. The Venn diagram for the left system looks like a globe with continents. So, let us call it the globe-system.
Lagard: That works, but how do we include rhombuses in the skyscraper system?
Fliba: I’m not sure. It seems hard since squares are types of rectangles and types of rhombuses but neither are all rhombuses rectangles not are all rectangles rhombuses.
Lagard: Are squares the only things which are both rectangles and rhombuses in this system?
Fliba: It seems that way. Let us assume that is true for now.
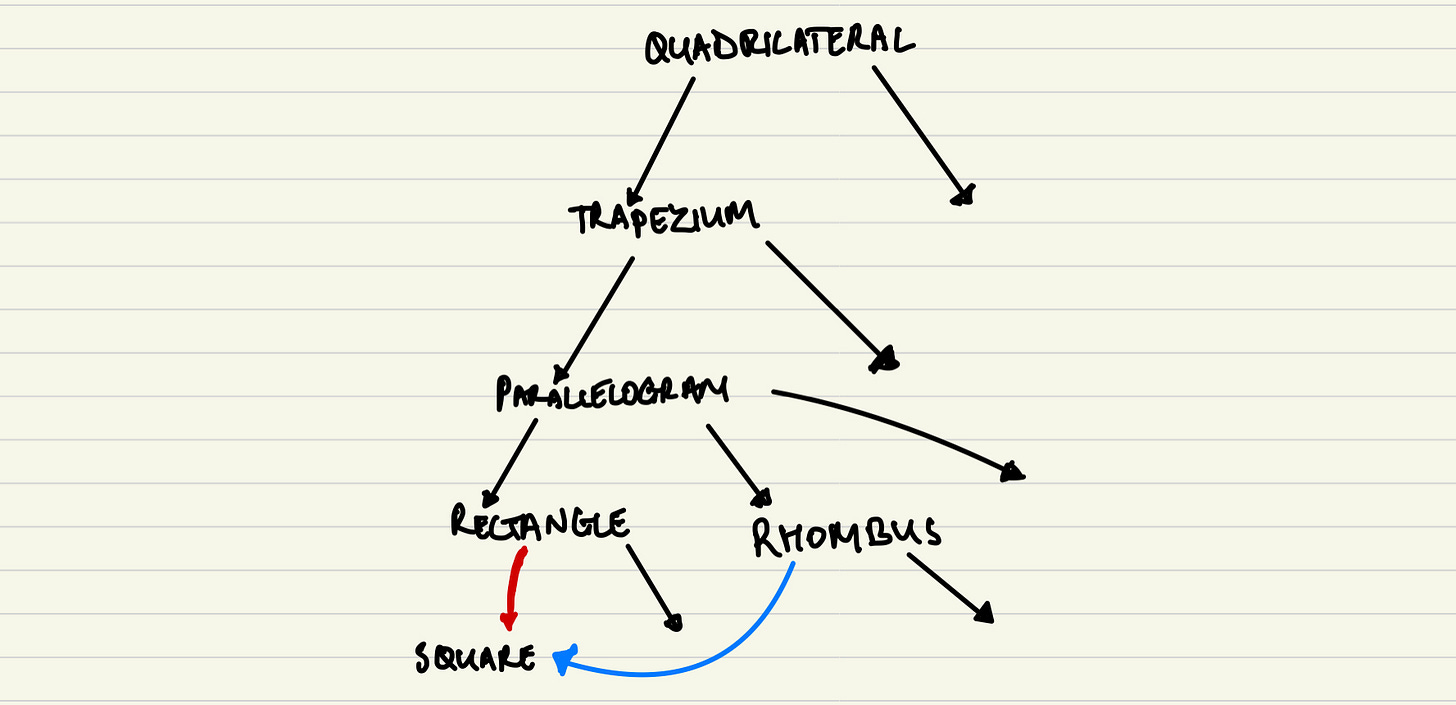
Lagard: I think I just thought of a way to do the Venn diagram for the skyscraper system. Let me draw it.
Fliba: That looks like it works. I still don’t see how we can translate this to the tree diagram. Let me message this to your sister Glagalbagal and ask her.
Can you translate the Venn diagram to a tree diagram? How is this new tree diagram different from the old one?
Fliba: She messaged back with this image:
She also said that this is not called a tree anymore in the language of something called Graph Theory. It has a different name, a DAG, but it doesn’t matter. I’m going to continue calling it a tree.
Lagard: That looks way more complicated than the globe system. Maybe this shows that the globe system is better?
Fliba: Let us not jump to a conclusion. We should do what we did last time and write out definitions. We can start with the globe system.
Lagard: Do any of the old definitions change?
Fliba: I think so. We had defined parallelograms as:
A parallelogram is a quadrilateral with opposite sides parallel and all angles not equal to 90 degrees.
This excludes rectangles but not rhombuses.
Lagard: So, we have to add in that all sides cannot be equal like they are for rhombuses.
Fliba: I think so. So, the definition of parallelogram becomes:
A parallelogram is a quadrilateral with opposite sides parallel, all sides not equal, and all angles not equal to 90 degrees.
Lagard: We also need to add in a definition of rhombuses. We must separate them from squares. How about:
A rhombus is a quadrilateral with opposite sides parallel, all sides equal, and not all angles are 90 degrees.
Fliba: I think that works. So, let us now try doing this in the skyscraper system.
What is a rhombus in the skyscraper system? Do any of the other definitions change? Think about that before reading on.
Lagard: In the skyscraper system, I don’t think any of the other definitions change since we do not need to separate rhombuses from the other shapes.
Fliba: That makes sense. But, what about the definition of a square? Isn’t a square now a rhombus with all angles 90 degrees?
Lagard: Yeah. You are right. But, it is also still a rectangle with all sides equal. So, while we do have a new definition for a square, the old definition remains.
Fliba: That is interesting. That means that rhombuses with all angles 90 degrees are the same as rectangles with all sides equal.
Lagard: That is weird. Why is that true?
Fliba: I think we should define rhombuses first before trying to answer that:
A rhombus is a parallelogram with all sides equal
Given the definitions of rectangle, parallelogram, and rhombus, think about why rhombuses with all angles 90 degrees is the same as rectangles with all sides equal.
Lagard: After seeing the definitions, it looks obvious why this is the case. What we add in to parallelograms to get rectangles is that all angles are 90 degrees, and what we add in to get rhombuses is that all sides are equal. So, a rectangle with all sides equal must be the same as a rhombus with all angles equal to 90 degrees.
Fliba: Nice! This classificatory system allowed us to learn something about these shapes which we may not have gotten from the other one. I think the skyscraper system is better.
Lagard: I agree. Another thing going against the globe system is that we had to change some definitions when we added in a new shape. That is annoying. Every time we want to add in a new shape, we will have to check all the other definitions to see what needs to change. In the skyscraper system, even though the diagrams look more complicated, they are easier to use.
This is the penultimate part of this series. In the final part, Fliba and Lagard will explore the relationship between classification in mathematics and other disciplines, focusing on biological classification.
There will also be future series that explore other aspects of classification.